Embark on an in-depth exploration of Unit 2 Worksheet 3 PVTN problems, a comprehensive guide that unravels the intricacies of this fascinating topic. Delving into the realm of problem-solving strategies, units and conversion, and the fundamental concepts of velocity, pressure, temperature, and number of moles, this resource empowers you with the knowledge and skills to tackle PVTN problems with confidence.

Through a systematic approach, this guide illuminates the relationships between these quantities using the ideal gas law, equipping you with a powerful tool for solving complex problems. Explore the practical applications of gas laws and Dalton’s law of partial pressures, gaining insights into their significance in chemistry and physics.

Problem-Solving Strategies

Problem-solving strategies are essential for effectively solving PVTN problems. These strategies involve understanding the problem statement, identifying the givens, organizing the problem, and simplifying it.

Steps to Solve PVTN Problems

1. Read the problem statement carefully and identify the givens.
2. Organize the givens and simplify the problem by identifying the relevant equations and concepts.
3. Solve the problem using the appropriate equations and principles.
4. Check the units and ensure they are consistent throughout the calculations.
5. State the final answer with the correct units.

Units and Conversion

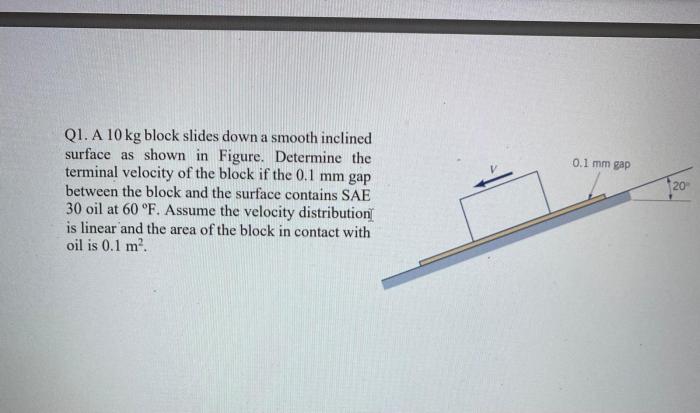
In PVTN problems, it is crucial to use consistent units. The most common units used are:

• Pressure: atm, mmHg, Pa
• Volume: L, mL
• Temperature: K, °C
• Number of moles: mol

Unit conversion is necessary to ensure consistency. The following conversion factors are commonly used:

• 1 atm = 760 mmHg = 101.3 kPa
• 1 L = 1000 mL
• K = °C + 273.15
• 1 mol = 6.022 x 10 ²³molecules

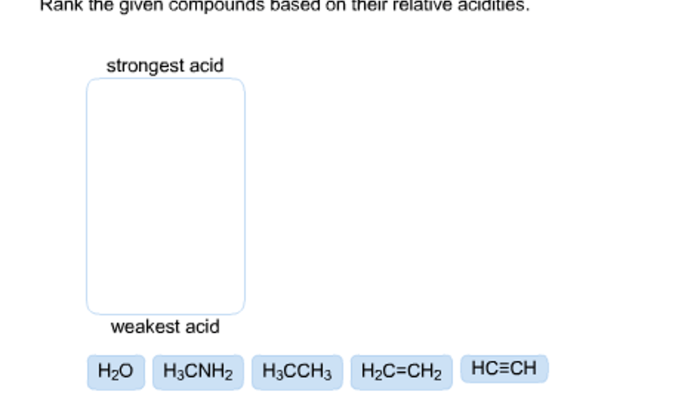
Velocity, Pressure, Temperature, and Number of Moles: Unit 2 Worksheet 3 Pvtn Problems

Velocity, pressure, temperature, and number of moles are the key variables in PVTN problems. They are related by the ideal gas law:

PV = nRT

where:

• P is pressure
• V is volume
• n is number of moles
• R is the ideal gas constant (0.0821 L atm / mol K)
• T is temperature

This equation can be used to solve for any of the variables if the other three are known.

Gas Laws and Their Applications

Boyle’s law, Charles’s law, and the combined gas law are three important gas laws that can be used to solve PVTN problems.

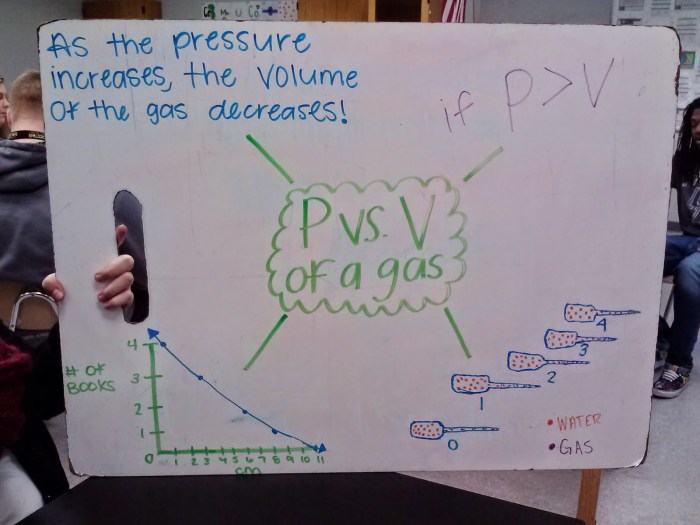
Boyle’s Law

Boyle’s law states that the pressure of a gas is inversely proportional to its volume at constant temperature.

P₁V ₁= P ₂V ₂

Charles’s Law, Unit 2 worksheet 3 pvtn problems

Charles’s law states that the volume of a gas is directly proportional to its temperature at constant pressure.

V₁/T ₁= V ₂/T ₂

Combined Gas Law

The combined gas law combines Boyle’s law and Charles’s law.

P₁V ₁/T ₁= P ₂V ₂/T ₂

Dalton’s Law of Partial Pressures

Dalton’s law of partial pressures states that the total pressure of a mixture of gases is equal to the sum of the partial pressures of each gas.

P_total= P ₁+ P ₂+ … + P _n

where P ₁, P ₂, …, P _nare the partial pressures of the individual gases.

Frequently Asked Questions

What are PVTN problems?

PVTN problems involve solving problems related to pressure, volume, temperature, and number of moles of gases.

How can I solve PVTN problems?

To solve PVTN problems, you need to understand the concepts of units and conversion, gas laws, and Dalton’s law of partial pressures.

What are the applications of PVTN problems?

PVTN problems have applications in various fields such as engineering, medicine, and environmental science.