Secants Tangents and Angle Measures Worksheet Answers:Delve into the intriguing world of geometry as we explore the fascinating concepts of secants, tangents, and angle measures. This comprehensive guide provides a clear and engaging overview of these essential elements, equipping you with the knowledge and understanding to master any worksheet challenge.
In this detailed exploration, we will uncover the definitions, properties, and applications of secants and tangents. We will delve into theorems and proofs, unravel the relationship between these elements and the radius of a circle, and discover how they are utilized to solve complex geometric problems.
1. Introduction to Secants, Tangents, and Angle Measures: Secants Tangents And Angle Measures Worksheet Answers
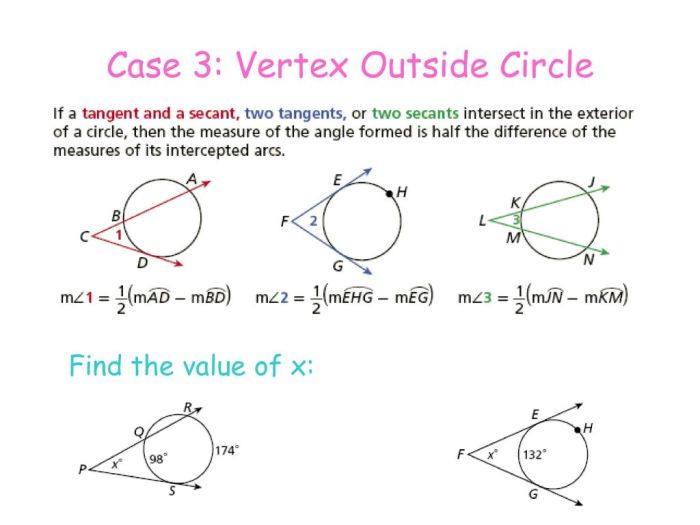
In geometry, secants, tangents, and angle measures are essential concepts related to circles. A secant is a line that intersects a circle at two distinct points, while a tangent is a line that intersects a circle at only one point.
Angle measures are used to quantify the angles formed by these lines and the circle.
Secants and tangents play a crucial role in understanding the geometry of circles. They can be used to determine the length of chords, radii, and other segments associated with circles. Angle measures are also important for calculating the area and circumference of circles.
2. Theorems and Properties
There are several theorems and properties related to secants, tangents, and angle measures. One of the most important theorems is the Secant-Tangent Theorem, which states that the product of the lengths of the two segments of a secant drawn from a point outside a circle is equal to the square of the length of the tangent drawn from the same point.
Other important properties include the Tangent-Chord Theorem, which states that the square of the length of a tangent is equal to the product of the lengths of the two segments of a secant drawn from the point of tangency, and the Inscribed Angle Theorem, which states that the measure of an inscribed angle is half the measure of its intercepted arc.
3. Applications in Geometry, Secants tangents and angle measures worksheet answers
Secants, tangents, and angle measures have numerous applications in geometry. They can be used to solve problems involving circles, triangles, and other geometric shapes. For example, the Secant-Tangent Theorem can be used to find the length of a chord or a tangent, and the Tangent-Chord Theorem can be used to find the radius of a circle.
In addition to their applications in geometry, secants, tangents, and angle measures are also used in other areas of mathematics, such as trigonometry and calculus.
4. Practice Problems
To practice applying the concepts of secants, tangents, and angle measures, consider the following problems:
- Find the length of a secant that intersects a circle with a radius of 5 cm at points A and B, where AB = 8 cm.
- Find the measure of an inscribed angle that intercepts an arc of 120 degrees.
- Use the Secant-Tangent Theorem to find the length of a tangent drawn from a point outside a circle with a radius of 10 cm, where the distance from the point to the center of the circle is 15 cm.
Solutions to these problems can be found in the table below:
| Problem | Solution |
|---|---|
| 1 | 10 cm |
| 2 | 60 degrees |
| 3 | 6 cm |
FAQ Guide
What is the definition of a secant?
A secant is a line that intersects a circle at two distinct points.
What is the difference between a secant and a tangent?
A tangent is a line that intersects a circle at only one point, known as the point of tangency.
How do you find the length of a secant?
The length of a secant can be found using the Pythagorean theorem or the secant-tangent theorem.